信任的进化博弈论 信任的进化博弈原理解析

信任的进化是一个博弈论游戏，那么这些博弈论是什么，他们各自的博弈原理又是什么？今天蕾米为大家带来信任的进化博弈论，信任的进化博弈原理解析，一起来了解一下游戏背后的哲理吧！

▍罪犯困境

这是本游戏的基本博弈模型，对此最经典的阐述为：两个嫌疑犯作案后被警察抓住，分别关在不同的屋子里接受审讯。警察知道两人有罪，但缺乏足够的证据。警察告诉每个人：如果两人都抵赖，各判刑一年；如果两人都招供，各判八年；如果两人中一个招供而另一个抵赖，坦白的放出去，抵赖的判十年。于是，每个囚徒都面临两种选择：招供或抵赖。然而，不管同伙选择什么，每个囚徒的最优选择是招供：如果同伙抵赖、自己招供的话放出去，抵赖的话判一年，招供比不招供好；如果同伙招供、自己也招供的话判八年，比起抵赖的判十年，招供还是比抵赖的好。结果，两个嫌疑犯都选择招供，各判刑八年。

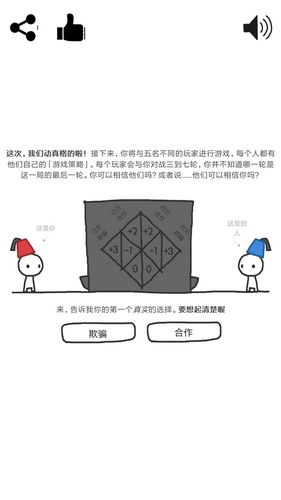
就像这个游戏机一样，当你投一个硬币进去，对方就会得到两枚硬币。显然，对于总体来说，选择合作得到的回报最高（每人失去1个，得到2个，总和4，增加2个），但对个人而言风险也是最大的（对方选择欺骗，你-1，对方3，总和2），所以在这种局面下，欺骗变成了最优策略。这样的局面，归根到底，是因为双方缺乏沟通而导致的。在无法信赖对手的一局游戏中，欺诈师往往会成为最后的赢家。有意思的是，囚徒困境推广到确定的N局游戏中也是成立的。原因如下：对于第N局，由于不用担心之后被报复（最后一局了嘛），最优策略显然是欺骗。对于第N-1局，由于已经知道了对方下一局的最优策略是欺骗，为了防止受到更多损失，最优策略显然也是欺骗。对于第N-2局，……所以，对于确定的N局游戏，最优策略永远是欺骗。

▍重复困境

这个升级版的囚徒困境源于一个全世界的重复囚徒困境竞赛（也是这个游戏的来源）。在这个竞赛中，许多博弈论专家将自己的策略编写成程序，和其它程序进行博弈（没错，游戏里的策略是其中的一些）经过很多很多轮竞赛后，出人意料的是，最佳确定性策略被认为是“以牙还牙”，这是阿纳托尔·拉波波特（Anatol Rapoport，《合作的进化》作者，也是竞赛的发起人）开发并运用到锦标赛中的方法。这个策略只不过是在博弈的开头选择合作，然后，采取对手前一回合的策略。

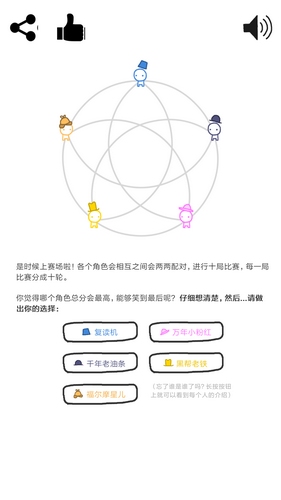
在完美的博弈中，复读机是最有效的。这种策略较好地规避了被欺骗的风险（被骗了还是要涨点记性），而对于合作者，显然双方都能获得较高的利润。而对于有可能失误的博弈（玩家准备合作，但是由于各种不可控因素造成背叛的结果），更好些的策略是“宽恕地以牙还牙”，即当你的对手背叛，在下一回合中你无论如何要以小概率（大约是1%~5%）时而合作一下。这是考虑到偶尔要从循环背叛的受骗中复原。至于更自由的博弈（可以选择对手），比较好的策略是：前几局选择合作进行试探，被多次欺骗后不再与此对手博弈（排挤掉欺诈师）

最终，博弈学家统计所有策略得到这样一个结论：最好的策略满足四个因素：友善，报复，宽容，不嫉妒。简单来说，表露合作的意向（让潜在的合作者与你合作），不盲目乐观（避免一直被欺诈师欺骗），适当包容小的失误（防止因误会导致的互相不信任），不追求比对手更高的得分（更高意味着恶性竞争）。因此，一些学者们据此得到一种给人以乌托邦印象的结论，认为自私的个人为了其自私的利益会趋向友善、宽恕和不嫉妒，即人人为我的社会可能建立在对利益的追求上。

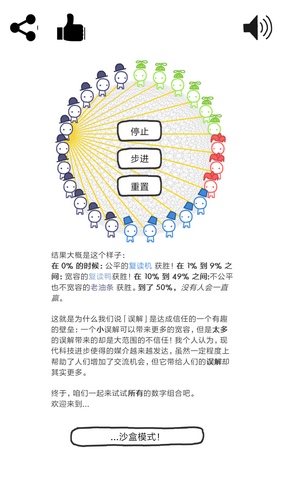
事实上，囚徒困境并不是那么简单，复读机也并不总是最终的赢家。在短期博弈上，最有效的往往是欺骗。在背叛的回报更高时，欺骗往往能获得最终胜利。在失误率过高时，结果趋于混沌。

以上就是蕾米为大家带来的信任的进化博弈论，更多精彩内容尽在信任的进化专区。

站住~游戏爱好者！我强烈建议你下个好游快爆APP。APP里有丰富的攻略秘籍，还有时下热门的爆款新游和实用工具，动起你的手指，与志同道合的朋友一起玩这个好玩的APP吧，快快快！